Maxima Manual

作成日　2007年8月19日

はじめに

　この文書はMaxima(マキシマ)の初心者を対象としたマニュアルである．Maximaとは数式処理ソフトウェアの1つであり，因数分解，数式の展開，微分方程式の解の導出，行列演算，グラフ描画など多くの機能を有する．さらに，多機能でありながらGNU Public License(GPL)の元に配布されている非商用ソフトウェアであり，誰でも自由に利用することができる．また，Maxima用のフロントエンド^※もいくつか提供されており，これを利用すれば数式を美しく出力することができる．

　本マニュアルでは，最初にMaxima，および，フロントエンドであるTeXmacs(テフマックス)のインストール方法について述べ，次にそれらの基本操作とMaximaプログラムについて述べる．そして，最後にはMaximaプログラムに関する演習問題を掲載する．

　　　なお，本マニュアルで紹介するのは，Maximaが持つ機能のごく一部である．Maximaについて更に詳しく知りたいときは以下のURLを参照されたい．

Maxima公式サイト：

http://maxima.sourceforge.net/

Maxima Manual(日本語訳)：

http://www.bekkoame.ne.jp/~ponpoko/Math/maxima/maxima.html

※ユーザーインタフェースを提供するプログラム

Maxima インストール

最初にMaximaのインストール方法について述べる．まず，Maximaのインストーラをダウンロードし，それを用いてインストール作業を行う．以下で，その手順を述べる．

1. インストーラのダウンロード

[1] Maxima公式サイト：http://maxima.sourceforge.net/ を開き，左側のメニューにある〔Download〕をクリックする．

図 1　Maxima公式サイト　Topページ

[２] Downloadsページの上方にあるリンク〔Sourceforge download page〕をクリック．

　 SOURCEFORGE.NETのMaxima Downloadページが開く．

図 2　Maxima公式サイト　Downloads ページ

[3] ページ下方にあるリンク〔maxima-5.12.0a.exe〕をクリックするとインストーラのダウンロードが始まる．

図 3　インストーラのダウンロード

Internet Explorerを使用している場合，ダウンロードが始まるとセキュリティ保護のメッセージが表示される．メッセージが表示された場合は，まずメッセージをクリックし，表示されるメニューの中の〔ファイルのダウンロード〕をクリック．すると，ファイルの処理に関するダイアログが表示されるので〔保存〕をクリックし，任意のフォルダにインストーラを保存する．

図 4　セキュリティ保護のメッセージ

図 5　ファイル処理に関するダイアログ

2. Maximaのインストール

[1] 1.でダウンロードした〔maxima-5.12.0a.exe〕をダブルクリック．ファイル実行の確認が表示されるので〔実行〕をクリック．

図 6　ファイルの実行に関するダイアログ

[2] Setup wizardが起動したら〔Next>〕をクリックし次ぎに進む．ライセンス規約が表示されるので，〔I accept the agreement〕にチェックを入れて次に進む．

図 7　セットアップウィザード

図 8　ライセンス規約について

[3] 以降，同様に〔Next>〕をクリックしインストールを進めていく．途中インストール先フォルダ等についての質問があるが，全て初期設定のままで良い．インストール内容の確認が表示されたら，〔install〕をクリックしMaximaのインストールを開始する．

図 9　インストール内容の確認

図 10　インストール実行中

[4] Maximaのインストールが終わるとREADMEファイルが表示される．ここでも，今まで同様に〔Next>〕をクリックし，最後に〔Finish〕をクリック，インストールウィザードを終了する．これで，Maximaのインストールは完了である．

図 11　インストールの完了

TeXmacsのインストール

　Maximaのインストールが終わったら，次はその出力結果を美しく表示するためのフロントエンドであるTeXmacsのインストールを行う．TeXmacsもMaxima同様にインストーラを用いてインストール作業を行う．

1. インストーラのダウンロード

[1] TeXmacs公式サイト：http://www.texmacs.org/ を開き，上側のメニュー

〔Download〕をクリックする．

図 12 TeXmaxs 公式サイト Top ページ

[２] Downloadページにあるリンク〔Windows〕をクリック．次に現れるページの上方にあるリンク〔WinTeXmacs〕をクリック．

図 13 TeXmaxs 公式サイト Download ページ

図 14　TeXmaxs 公式サイト Windows ページ

[3] 　リンク〔wintexmacs-1.0.5.exe〕をクリックする．Maximaインストール時と同様に，任意のフォルダに保存する．

図 15 TeXmacs インストーラのダウンロード

2. TeXmacs のインストール

　[1] 〔wintexmacs-1.0.5.exe〕をダブルクリックして開く．Setup Wizardが起動するので〔Next>〕をクリックして次へ進む．

図 16 セットアップウィザード

　[2] ライセンス規約が表示されるので，〔I accept the terms in the license agreement〕　　

　　にチェックを入れた後で，〔Next>〕をクリックし次に進む．

図 17　ライセンス規約について

[3] 以降，同様に〔Next>〕をクリックしインストールを進めていく．途中インストール内容等についての質問があるが，全て初期設定のままで良い．インストール先の設定画面が表示されたら，〔install〕をクリックしインストールを開始する．

図 18　インストール先の設定画面

図 19　インストール実行中

[4] インストール完了のメッセージが表示されたら〔Finish〕をクリック，インストールウィザードを終了する．

図 20　インストールの完了

3. 設定ファイル自動生成

TeXmacsの初回起動時に，以下のメッセージが表示される．〔はい(Y)〕をクリックすると設定ファイルが自動生成される．このときに既にMaximaがインストールされていれば，それを使用するための設定も自動で実行される．

自動生成には多少時間がかかる．もし，途中でフリーズしたと勘違いし強制終了させてしまうと，TeXmacs上でMaximaが起動しなくなる場合があるので注意すること．

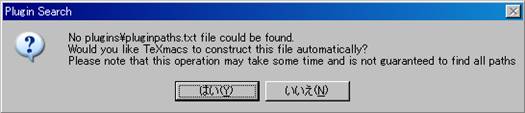
図 21　設定ファイルの自動生成

　TeXmacsを使用すると，数式が美しく表示されるメリットがある，しかし，計算が遅くなる，複雑な計算に対応できなくなる，操作性が悪くなる等のデメリットもあるので，使用するか否かは各自の判断に任せる．

Maximaの基本操作

1. Maximaの起動

　まず，TeXmacsを使わずにMaximaを使用する方法について述べる．上記の方法でMaximaをインストールすると3つのMaxima実行環境を利用することができる．ここでは，XMaximaというプログラムを用いてMaximaプログラムを実行する方法について述べる．

XMaximaを起動するためには，スタートメニューから〔プログラム〕⇒〔Maxima-5.12.0〕⇒〔XMaxima〕の順にクリックする．すると，以下のようにXmaximaが立ち上がる．

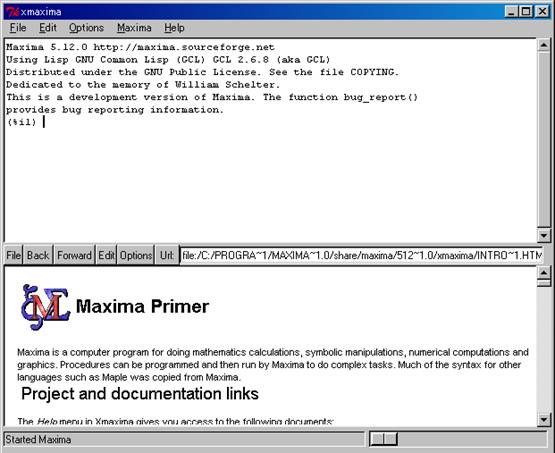
図 22　XMaximaの起動

2. Maximaプログラムの実行

Maximaプログラムを実行する方法は，プログラムを1行ずつ実行する方法，あらかじめプログラムをファイルに記述しまとめて実行する方法の２つがある．

2-1 1行ずつ実行する

1行ずつ実行結果を確認しながら実行する場合は，(%i1)の後にプログラムを記述し，〔Enter〕キーを押して実行すればよい．以下にプログラムの入力例を示す．この例はの解を求めるプログラムである．

<入力例>

　(%i1)以下を入力し〔Enter〕キーを押して実行すると次の出力結果が得られる．

<出力例>

2-2　ファイルから実行する

ファイルからプログラムを実行する場合は次の手順を踏む．

[1] あらかじめ適当なテキストエディタを用いてプログラムを記述し拡張子を.mcとして保存する．

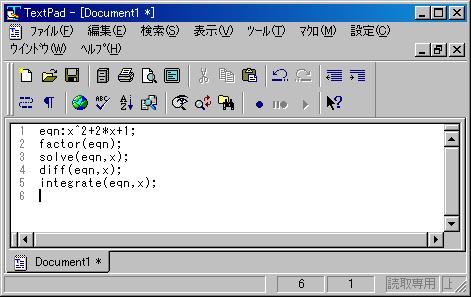
図 23 テキストエディタ例

[2] ツールバーから〔File〕⇒〔Batch File〕の順にクリックする．.mcとして保存したファイルを開けば実行開始する．

図 24　プログラムの実行

　以下にMaximaプログラム例を示す．このプログラムはに関する，因数分解，方程式の解，微分，積分を順に求める例である．適当なテキストファイルを開き，Maximaプログラム例をコピーし貼り付けよ．そして上記の手順で実行すると順に結果が出力されるので各自確認されたい．

<入力例>

3. その他の操作

3-1. プログラムの強制終了

プログラムが終了しない場合などは，キーボードで〔Ctrl〕+〔g〕を押せば実行中のプログラムを強制終了することができる．

3-2. 定義した変数，関数等の消去

　前に実行したプログラムにて使用した変数や関数などの設定を消去せずに，次の計算を行うと，それが計算間違いの原因につながる．そこで，新たな計算を行う前にそれらを消去する必要がある．そのためには，ツールバーから〔Maxima〕⇒〔Clear Memory〕⇒　　〔Kill All〕の順にクリックする．

図 25　変数，関数等の消去

3-3. Maximaの再起動

　何か問題が生じたとき再起動が必要になる場合がある．XMaximaではウィンドウを閉じずにMaximaを再起動することができる．再起動するためにはツールバーから　　　　〔File〕⇒〔Restart〕の順にクリックする．

図 26　再起動

4. XMaximaの終了

　XMaximaを終了する場合，右上の〔×〕をクリックする．

図 27　XMaximaの終了

TeXmacsの基本操作

1. TeXmacs上でのMaximaの起動

TeXmacs上でMaximaを動作させる方法について述べる．この場合，XMaximaのように，ファイルからのプログラム実行，プログラムの強制終了や，ウィンドウを閉じずに再起動するなどの機能は使えない．Maximaの起動手順を以下に示す．

[1] スタートメニューから〔WinTeXmacs〕を起動する．

[2] ツールバーから〔Insert〕⇒〔Session〕⇒〔Maxima〕の順にクリックする．

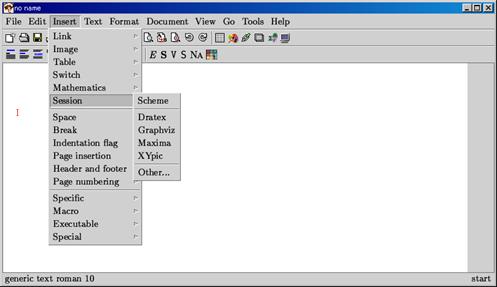
図 28　TeXmacsの起動

[3] 以下の画面が表示されたら起動完了である．

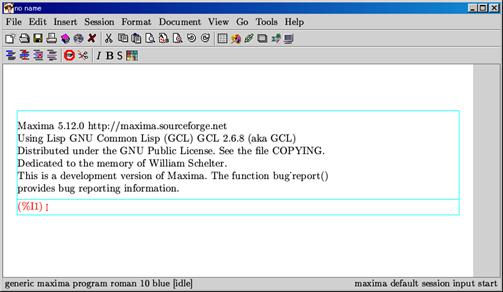
図 29 Maximaの入力画面

2. TeXmacsの終了

　TeXmacsのウィンドウ右上の〔×〕ボタンをクリックし終了する．保存してない場合，〔There are unsaved file. Really quit?〕というメッセージが表示される．終了してよければキーボードで〔y〕を入力し〔Enter〕キーを押す．

　

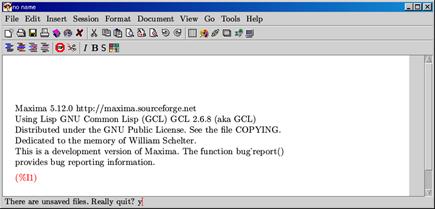
図 30　Maximaの終了

Maximaプログラム

ここでは，Maximaプログラムについての解説を行う．各解説にはそれぞれMaximaプログラム例を示している．このMaximaプログラム例における，実行結果は表示の美しいTeXmacsの表示にあわせる．ただし，現在のTeXmacsのバージョンにはバクがあり，アルファベットの大文字が小文字に，小文字が大文字になっているので注意して欲しい．

1. 基本演算

Maximaでは以下の演算子を用いて，四則演算，指数乗を行うことができる．

表1　演算子

記号	意味
+	加法
-	減法
*	乗法
/	除法
^	指数乗

<Maximaプログラム例1>

ここで，除算の結果が分数のまま扱われていることに注目してほしい．Maximaはできる限り正確な値を計算できるような工夫がされている．分数がそのまま分数として扱われるのもその工夫の1つである．もちろん，小数で解を表示することも可能である．その方法は6 -4にて示す．

2. 入力の区切り

上記のMaximaプログラム例を見ると各入力の末尾に〔;〕がある．これはMaximaプログラムにおいて各入力の区切りを示す記号である．入力を区切るための記号には，以下の2種類があり，使用する記号によって出力結果を表示するか否かが決まる．

表2　入力の区切り

記号	意味
;	入力の区切りを示す．出力結果を表示する場合に用いる
$	入力の区切りを示す，出力結果を表示しない場合に用いる

<Maximaプログラム例2>

この例のように〔;〕を利用した場合は次に出力結果が表示されている．それに対し，〔$〕を使用した場合は出力結果が表示されずに，次の入力待ち状態になる．

3. 入力，出力内容の参照

　事前に入力した内容，または出力した内容を参照することができる．参照するためには表3のように記述する．なお，表3においてxxは参照したい入力を示す番号である．

表3　入力，出力内容の参照

記号	意味
%ixx	入力%ixxを再実行する
%oxx	出力%oxxを参照する
%	直前の入力を再実行する

<Maximaプログラム例3>

4. 変数

4-1 変数の基本的利用法

Maximaで変数を利用する場合，前もって宣言をする必要は無い．次のように記述すれば，ある文字(または文字列)を数値に置き換えることができ，それを変数のように利用することができる．

　また，数値だけでなく式を代入することもできる．式を代入する場合は以下のように記述する．

この変数の利用方法を見てわかるとおり，Maximaプログラムにおいて〔:〕は左側のものを，右側のものに置き換えるという意味を持つ．

<Maximaプログラム例4>

変数を消去したい場合は次のように記述すれば，変数は単なる文字に戻る．

　以下に，このkill関数の使用例として，Maximaプログラム例3のaとbを削除する例を示す．

<Maximaプログラム例5>

　最初はaとbを表示すると，先ほど代入した値，および，式が表示される．しかしkill関数実行後は単なる文字に戻っているのがわかる．

4-2 配列変数

Maximaでは最大5次元までの配列変数を使うことができる．配列変数の利用方法は，あらかじめ配列変数を生成した上で利用する方法と，生成せずに値を代入し利用する方法の2つがある．

配列変数の生成はarray関数を用いて行う．

配列の要素数は引数で渡す最終要素番号により決まる．要素番号は0から始まるため，1なら2つ，2なら3つの要素を持つ配列が生成される．各要素に値を代入したい場合は次のように記述する．

配列の要素はlistarray関数を用いて参照できる．

<Maximaプログラム例6>

　この例は3×3の2次元配列を生成し値を代入後，listarray関数で配列要素を確認しているものである．値が代入されていない要素は〔#####〕として表現されている．次に，配列をあらかじめ生成せずに配列を利用する例を示す．

<Maximaプログラム例7>

　この例のように要素の値を与えるだけで配列を利用することができる．この場合，listarray関数は代入された値のみを返す．配列の要素数を動的に変更したい場合はこの方法で配列を利用すると良い．

5. 関数

Maximaプログラムでは関数を定義することもできる． 関数定義の方法は2通りある．1つ目は〔:=〕を用いた方法である．

この方法では場合によって，問題が生じる場合がある．関数の利用例を以下に示す．

<Maximaプログラム例8>

この例に出てくるsin関数，および，diff関数についての詳細は後に述べる．sin関数は角度[rad]を受け取りsin関数の結果を返すもの，diffは微分を行う関数で，この例ではsin(x)をxに関して微分しているとだけ理解して欲しい．なお，円周率は%piと入力することで得られる．

ここで，(%I1)で定義した関数は(%I2)の結果にて正常に機能しているのが確認できる．しかし，(%I3)で定義した関数は，(%I4)にて実行されているが，エラーメッセージが表示されている．エラーの原因は代入後に微分が行われたことである．diff関数に式でなく数値が渡されるとエラーが表示される(フロントエンドを利用しない場合，結果は0となる)．

　このエラーを避けるためには次のように，define関数を用いて関数を定義すればよい．

　Maximaプログラム例8の(%I3)以下を，define関数を用いて実行した例を以下に示す．

<Maximaプログラム例9>

今度は先に微分が行われ，正常に関数の実行結果が表示されている．

6. 数式の操作

6-1 展開

方程式の展開をする場合はexpand関数を用いる．

<Maximaプログラム例10>

6-2 因数分解

多項式を因数分解するには，factor関数を用いる．

<Maximaプログラム例11>

6-3 方程式の解

代数方程式はsolve関数を用いて解くことができる．

<Maximaプログラム例12>

ここで，exp(x)は指数関数である．この例において，(%I1)は正しく解が求められている．しかし，(%I2)の出力結果を見ると右辺にxが残っており，解が求められたとは言えない．それでも解を求めたいときは，Newton法を用いて，数値的に解を近似することができる．

まず，Newton法を用いるために必要なパッケージを読み込む．

　パッケージを読み込んだら，Newton法を用いて計算する．

　それでは，以下にMaximaプログラム例12 (%I2)をNewton法を用いて解いた例を示す．

<Maximaプログラム例13>

このように，近似解を求めることができた．ここで，(%O2)の下つき文字Bは次の6-4にて述べるbfloat関数が内部で呼び出されており，fpprecで指定された有効桁数で表示されていることを示す．

6-4 数値解

数値解を知りたい場合はfloat関数を用いる．float関数だけを用いた場合，式が展開されない式が残る場合があるのでexpand関数と組み合わせて用いるほうがよい．

<Maximaプログラム例14>

　float関数は方程式の数値解だけでなく，分数を小数近似することもできる．

また，任意の精度で数値解を求めたいときは，グローバル変数で定義されているfpprecに有効桁数を設定したあと，bfloat関数を用いて数値解を求める．

<Maximaプログラム例15>

7. 各種計算用関数

7-1 平方根

　sqrt関数を用いて平方根の計算ができる．

<Maximaプログラム例16>

7-2 絶対値

絶対値はcabs関数を用いて計算できる．

<Maximaプログラム例17>

ここで，(%I2)で入力している%iは虚数単位を意味する．

7-3 三角関数

Maximaには以下の三角関数，および，それに対応する逆三角関数が用意されている．引数である角度はいずれも[rad]で与える．

<Maximaプログラム例18>

7-4 対数関数

自然対数はlog関数を用いて計算できる．

　常用対数はlog10関数を用いて計算できる．log10関数を使用する場合は最初にパッケージを読み込む．

<Maximaプログラム例19>

(%I1)は自然対数の算出例である．(%I2) (%I3)では，log10パッケージを読み込み，常用対数を計算している．

8. 微分と積分

8-1 極限

極限の計算にはlimit関数を用いる．

　近づける値に∞または−∞を指定したい場合は以下のように表記する．

表4　∞，−∞の表記

表記	意味
inf	∞
minf	−∞

<Maximaプログラム例20>

8-2 微分

微分の計算にはdiff関数を用いる．階数が1の場合は省略可能である．

　また，単なる変数を，ある変数に依存する関数にしたい場合depends関数を用いる．

<Maximaプログラム例21>

　(%I1)は2階の微分の例である．(%I2)，および，(%I3)では最初にxをtに依存する関数として指定し，その後でsin(x)をtについて微分している．

8-3 積分

積分の計算はintegrate関数を用いる．不定積分，定積分はそれぞれ以下のように記述する．

定積分の場合，実行時に次のメッセージが表示される場合がある．

　これは関数の値が正負を確認するメッセージであり，正の場合〔p;〕，負の場合〔n;〕を入力し〔Enter〕キーを入力すれば，定積分の結果が出力される．

<Maximaプログラム例22>

8-4 微分方程式の解

微分方程式の解はatvalue関数で初期値を与えた後，desolve関数を用いて求める．

　以下にMaximaを用いて放物運動に関する微分方程式を解いた例を示す．水平面上にx，y軸をとり，それらの鉛直上方にz軸を取る．地上の一点から水平面に対しθ度の方向に，xｚ面上に沿って，初速度で物体を投げ上げる．このときの物体の加速度は以下の通りになる．

この解をMaximaにより解く．なお，初期条件としてt=0における物体の位置，および，速度を以下のように与える．

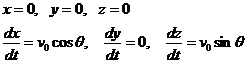
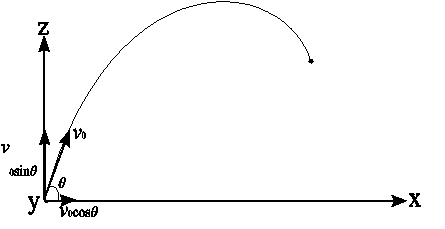
図24 放物運動

<Maximaプログラム例23>

　ここで，出力結果にθが現れている．これはTeXmacsの機能によるもので，thetaと入力すると自動でθに変換されて表示される．この例ではatvalueで初期値を与えた後，desolveを実行し(%O7)，(%O8)，(%O9)でx,y,z軸方向それぞれに関する解が求められている．なお，desolveの引数はx(t)のように，関数と変数の関係を明示的に表さなくてはならない．

　このdesolveでは解けない微分方程式も多く存在する．そのような微分方程式に対してはode2関数を用いれば解ける場合がある．

ode2は様々な解法を機能として持ち，解の導出に失敗するたびに別な解法を用いて導出しようと試みる．また，desolveと違い，関数と変数の関係を明示的に表す必要はない．

<Maximaプログラム例24>

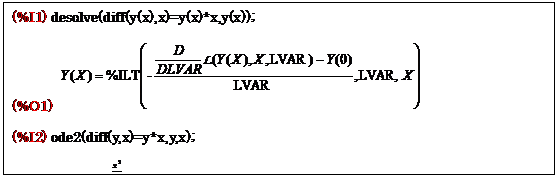
　これは，微分方程式を解いた例である．まず (%I1)ではdesolveを用いて解の導出を試みている．しかし，内部で呼ばれている関数が残った意味不明な解が出力されている．それに対して，(%I2)のode2関数を用いた例では正しい解が算出されている．

9. 線形代数

9-1 ベクトル(リスト)

maximaではリストとしてベクトルを表現することができる．

　リストの要素を参照したい場合は次のように記述する．リスト全体の要素を参照したい場合は，リスト変数名を記述すればよい，各要素を参照する場合は要素番号を指定する．

<Maximaプログラム例25>

9-2 行列

行列を使いたい場合はmatrix関数を用いる．

　また，単位行列はident関数を用いて生成することができる．

行列の要素を参照する方法を以下に示す．上から，要素全体を参照する方法，行ごとに参照する方法，列ごとに参照する方法，各要素ごとに参照する方法である．

　transpose関数については9-4に述べる．

<Maximaプログラム例26>

9-3 余因子行列

余因子行列はadjoint関数を用いて計算する．

<Maximaプログラム例27>

9-4 転置行列

　転置行列はtranspose関数を用いれば得られる．

<Maximaプログラム例28>

9-5 逆行列

　逆行列はinvert関数を用いて計算される．

<Maximaプログラム例29>

2-6 内積, 外積

　内積は〔.〕を用いて計算される．

　Maximaには外積を計算する関数等は用意されていない．外積を計算する方法は，外積の定義に従って以下のように計算すればよい．

ここで，v1,v2は3次元ベクトルである．また次のように記述しても外積を計算できる．

<Maximaプログラム例30>

この例は3次元ベクトルv1とv2の内積および外積を求めた例である．ただし，TeXmacs上でMaximaを使用している場合は行列計算に弱くなるようで，(%I4) (%O5)の計算はエラーとなり計算されない．この計算をしたいときはXMaximaを用いて計算すること．

9-7 連立方程式

　連立方程式は既に解説したsolve関数を用いて計算できる．

<Maximaプログラム例31>

10. ループ計算と条件分岐

10-1 for文

　ループ計算にはfor文を用いる．for文は以下の2つの記述法があり，前者は終了値が満たされるまでループし，後者は条件式が満たされるまでループされる．

10-2 if文

条件分岐を作成したい場合はif文を使う．

条件式には次の演算子を利用することができる．

表4　演算子

記号	意味
=	等しい
#	等しくない
<>	未満,越える
<= >=	以上,以下

　複数の条件式を用いる場合andとor が用意されている．

<Maximaプログラム例32>

11. グラフの描画

グラフは以下のplot2d関数を用いて計算することができる．

<Maximaプログラム例33>

　このプログラムを実行すると，グラフ描画ソフトであるgnuplotが立ち上がり，図31のグラフが描画される．

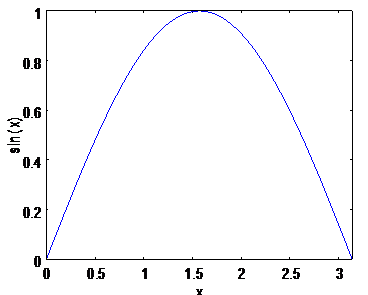
図 31 グラフ描画例

12. データファイルの利用

　Maximaにはファイル入出力用の関数がいくつか用意されている．ここでは，csv形式のファイルをリストとして読み込む方法，および，リストまたは行列の内容をcsv形式で出力する方法を述べる．

　まず，この機能を使用するためには，以下のようにパッケージを読み込む

　このパッケージを使うと次の関数が利用できるようになる．

この関数は上から，ファイルの内容をリストとして読み込む関数，行列として読み込む関数，行列，または，リストの内容をファイルに書き込む関数である．ただし，この関数を利用する場合，TeXmacsを利用すると正常にファイルを読み書きできないことがあるため，XMaximaを使うことをお勧めする．

次に，このパッケージを利用した例を次に示す．この例を実行する前に以下のcsvファイルを用意し，Cドライブ直下にtest.csvという名前で保存しておくこと．

<test.csv>

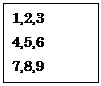
<Maximaプログラム例34>

この例では，まず，test.csvをリスト，および，行列として読み込んでいる．次に，読み込んだ内容を，Cドライブ直下にwrite_test1.csv，および，write_test2.csvというファイルに書き出している．

13. その他の関数

　Maximaはこのマニュアルで紹介した機能以外にも様々な機能を有する．最後に，その中から最小二乗法を計算するための関数lsquaresを紹介する．

　ここで，数値行列は変数の値を入れた行列である．

<Maximaプログラム例35>

演習問題

<代数方程式>

問1 次の数式を展開せよ．

　(1) 　　(2) (3)

問2 次の数式を因数分解せよ．

　(1) 　　(2) (3)

問3 次の代数方程式の解を求めよ．

　(1) 　　(2) (3)

<微分・積分>

問4 次の関数を微分せよ．

　(1) 　　(2) (3)

問5 次の不定積分の値を求めよ．

　(1) (2) (3)

問6 次の関数の定積分の値を求めよ．

　(1) 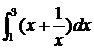(2) (3)

<微分方程式>

問7 次の微分方程式の解を求めよ．

　(1) (2) (3)

<行列>

問8 　

のとき，以下の行列を計算をせよ．

(1) (2) (3) (4) (5)

<グラフ>

問9　<Maximaプログラム例21>の運動方程式をもとに，物体の軌跡を描画せよ．

<応用問題>

問10　図22に示す3自由度ロボットマニピュレータにおいて，各関節角度と先端位置の関係を表現した順運動学方程式を求めるMaximaプログラムを構築せよ．

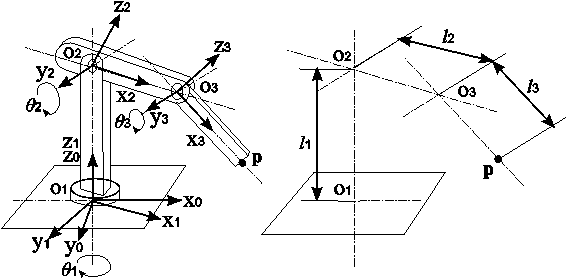
図22　ロボットマニピュレータ

演習問題　解答プログラム例

問1

(1) expand((x+a)*(x+b));

(2) expand((x+2)^2);

(3) expand((x+2)^2);

問2

(1) factor(x^2+(a+b)*x+a*b);

(2) factor(x^2-x-6);

(3) factor(x^3+3*x^2*y+3*x*y^2+y^3);

問3

(1) solve(a*x^2+b*x+c=0,x);

(2) solve(x^2+2*x+1=0,x);

(3) solve(2*x^2+x-3);

問4

(1) diff(x^2+2*x+2,x);

(2) diff(sin(x-3)^2,x);

(3) diff(log(x*(x+3)),x);

問5

(1) integrate((x+2)/((x-1)*(x-3)),x);

(2) integrate(cos(2*x+1),x);

(3) integrate(log(x)^2,x);

問6

(1) integrate((x+1/x),x,1,3);

(2) integrate(sin(x),x,0,%pi/2);

(3) integrate(log(x^2+1),x,0,1);

問7

/*yをxに依存する関数にする*/

depends(x,y);

(1) ode2(x*diff(y,x)+y=0,y,x);

(2) ode2((x^2-x*y)*diff(y,x)=0,y,x);

(3) ode2(x*diff(y,x)-y=x*(1+2*x^2),y,x);

問8

/*行列の定義*/

A:matrix([a,b],[c,d]);

B:matrix([e,f],[g,h]);

(1) A+B;

(2) A-B;

(3) A.B;

(4) invert(A);

(5) transpose(A);

問9

atvalue(x(t),t=0,0);

atvalue(y(t),t=0,0);

atvalue(z(t),t=0,0);

atvalue(diff(x(t),t),t=0,v0*cos(theta));

atvalue(diff(y(t),t),t=0,0);

atvalue(diff(z(t),t),t=0,v0*sin(theta));

g:9.81;

theta:45;

v0:100;

x:desolve(diff(x(t),t,2)=0,x(t));

z:desolve(diff(z(t),t,2)=-g,z(t));

plot2d([parametric, x,z,[t,0,100]]);

plot2d([parametric, x,z,[t,0,10]]);

問10

/* 同次変換行列の定義 */

H1:matrix([cos(theta1), -sin(theta1), 0,0],[sin(theta1),cos(theta1),0,0],[0,0,1,0],[0,0,0,1]);

H2:matrix([cos(theta2),0,-sin(theta2),0],[0,1,0,0],[sin(theta2),0,cos(theta2),l1] ,[0,0,0,1]);

H3:matrix([cos(theta3),0,-sin(theta3),l2],[0,1,0,0],[sin(theta3),0,cos(theta3),0] ,[0,0,0,1]);

/* x3y3z3座標系から見たpの定義*/

p:transpose( [l3,0,0,1] );

/*運動学方程式の導出*/

H1.H2.H3.p;